Edge cover
In graph theory, an edge cover of a graph is a set of edges such that every vertex of the graph is incident to at least one edge of the set. In computer science, the minimum edge cover problem is the problem of finding an edge cover of minimum size. It is an optimization problem that belongs to the class of covering problems and can be solved in polynomial time.
| Covering-packing dualities | |
| Covering problems | Packing problems |
|---|---|
| Minimum set cover | Maximum set packing |
| Minimum vertex cover | Maximum matching |
| Minimum edge cover | Maximum independent set |
Contents |
Definition
Formally, an edge cover of a graph G is a set of edges C such that each vertex is incident with at least one edge in C. The set C is said to cover the vertices of G. The following figure shows examples of edge coverings in two graphs.
A minimum edge covering is an edge covering of smallest possible size. The edge covering number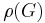 
is the size of a minimum edge covering. The following figure shows examples of minimum edge coverings.
Note that the figure on the right is not only an edge cover but also a matching. In particular, it is a perfect matching: a matching M in which each vertex is incident with exactly one edge in M. A perfect matching is always a minimum edge covering.
Examples
- The set of all edges is an edge cover, assuming that there are no degree-0 vertices.
- The complete bipartite graph Km,n has edge covering number max(m, n).
Algorithms
A smallest edge cover can be found in polynomial time by finding a maximum matching and extending it greedily so that all vertices are covered.[1][2] In the following figure, a maximum matching is marked with red; the extra edges that were added to cover unmatched nodes are marked with blue. (The figure on the right shows a graph in which a maximum matching is a perfect matching; hence it already covers all vertices and no extra edges were needed.)
On the other hand, the related problem of finding a smallest vertex cover is an NP-hard problem.[1]
See also
- Vertex cover
- Set cover – the edge cover problem is a special case of the set cover problem: the elements of the universe are vertices, and each subset covers exactly two elements.
Notes
- ^ a b Garey & Johnson (1979), p. 79, uses edge cover and vertex cover as one example of a pair of similar problems, one of which can be solved in polynomial time while the other one is NP-hard. See also p. 190.
- ^ Lawler, Eugene L. (2001), Combinatorial optimization: networks and matroids, Dover Publications, pp. 222–223, ISBN 9780486414539, http://books.google.com/books?id=m4MvtFenVjEC&pg=PA222.
References
- Weisstein, Eric W., "Edge Cover" from MathWorld.
- Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1045-5.